Die Berechnung des Gleichgewichtszustands kann als Optimierungsproblem mit konvexer Zielfunktion und linearen Nebenbedingungen folgendermaßen formuliert werden:

Dabei gilt Folgendes:
|
E |
Menge aller Kanten im Netz und a eine dieser Kanten |
|
qa |
Belastung von Objekt a |
|
Ra(x) |
Widerstand von Objekt a bei Belastung x (monoton steigend in x) |
|
qij |
gesamte Nachfrage (Anzahl Fahrten) von Bezirk i nach Bezirk j |
|
qijr |
Belastung der Route r von Bezirk i nach Bezirk j |
|
Pijr |
Route r von Bezirk i nach Bezirk j |
|
E+u |
Menge der eingehenden Kanten an Knoten u |
|
E-u |
Menge der ausgehenden Kanten an Knoten u |
|
Du |
Zielverkehr von Knoten u |
|
Ou |
Quellverkehr von Knoten u |
Kanten sind in Visum alle Strecken, Abbieger und Anbindungen, Knoten sind Bezirke und Netzknoten.
Die Zielfunktion minimiert das Integral der Widerstände aller Netzobjekte. Die Nebenbedingungen besagen Folgendes (von oben nach unten):
- Alle Wegebelastungen müssen positiv sein.
- Die Belastungen aller Wege von Bezirk i nach j müssen sich zur Gesamtnachfrage von i nach j addieren.
- Die Belastung einer Kante ergibt sich als Summe der Belastungen aller Wege, die diese Kante enthalten.
- An jedem Knoten gilt Flusserhaltung. Wenn ein Knoten einem Bezirk entspricht, muss die Differenz zwischen den Belastungen aller eingehenden Kanten und den Belastungen aller ausgehenden Kanten exakt der Differenz zwischen dem Ziel- und Quellverkehr entsprechen. An Netzknoten gibt es keinen Quell- und Zielverkehr, folglich muss die Differenz null sein.
Das Optimierungsproblem wird wegen der nichtlinearen Zielfunktion nicht direkt, sondern iterativ gelöst, wobei wegen der Monotonie der Widerstandsfunktion das Minimum dadurch erreicht wird, dass ausgehend von einer Startlösung Belastung zwischen den alternativen Wegen einer Fahrbeziehung i-j verlagert wird, sodass auf den Wegen gleicher Widerstand herrscht.
Während der Gleichgewichtsumlegung werden die in Abbildung 96 gezeigten Schritte durchlaufen.
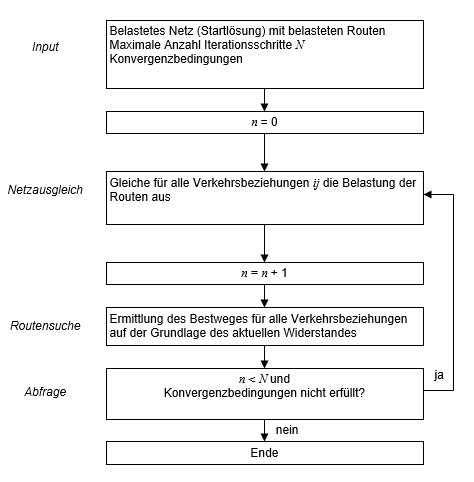
Abbildung 96: Ablauf Gleichgewichtsumlegung
Ausgehend von einer Alles-oder-Nichts-Umlegung als Startlösung, wird der Gleichgewichtszustand in einer mehrstufigen Iteration hergestellt. Im inneren Iterationsteilschritt, dem Ausgleichen, werden Belastungen einer Beziehung von Routen mit hohen Widerständen auf Routen mit geringen Widerständen verschoben. Jede Verlagerung von Fahrzeugen von einer Route auf eine andere Route wirkt sich auf die Widerstände der überfahrenen Netzobjekte aus.
In der äußeren Iteration wird überprüft, ob aufgrund des aktuellen Netzzustands neue Routen mit geringeren Widerständen gefunden werden können. Ist das für mindestens eine Beziehung der Fall, muss wieder ein Netzausgleich berechnet werden.
Das Verfahren wird beendet, wenn die Konvergenzbedingung, standardmäßig das Gap, erfüllt ist bzw. die maximale Anzahl von Iterationen erreicht ist.
Alternativ zu der Bestwegumlegung am Beginn kann auch auf das Ergebnis einer existierenden statischen Umlegung aufgesetzt werden.

